
Escalas
Contenido
Escalas mayoresEscalas menores
Escalas relativas
Alteraciones contenidas en escalas
Armaduras
La escala menor armónica
La escala menor melódica
Comparación de escalas
Deducción de la tonalidad de una melodía
Como hemos mencionado con anterioridad, una escala es un conjunto de notas ordenadas de acuerdo a su frecuencia. Son muy importantes porque sus notas son el material fundamental para la creación de música.
En la página dedicada a las notas musicales generamos la siguiente escala cromática igualmente temperada para Do:

Esta escala contiene todas las notas necesarias para la construcción de las escalas a considerar en esta página. Las notas a colores son las correspondientes a la escala mayor de Do sobre la octava que va de C4 a C5. En lo siguiente se consideran las escalas sobre una octava, pero sin hacer referencia a las octavas consideradas, y en consecuencia tampoco a las frecuencias.
Escalas mayores
Las escalas mayores son la base sobre la cual se construye gran parte de la teoría de la música en la civilización occidental. Usaremos la escala mayor de Do como punto de partida para generar las escalas mayores para otras tonalidades y otros tipos de escala. Esta escala tiene la siguiente conformación:

De acuerdo a esta figura, si un avance de un semitono sobre la escala se representa por S y el avance de un tono se representa por T, la fórmula para la creación de escalas mayores es:

La figura anterior introduce un nuevo concepto, el de grado de la escala. Cada una de las notas de la escala corresponde a un grado de la misma, los cuales se identifican mediante números romanos. Cada grado de la escala recibe un nombre propio que indica en cierta medida su posición y función dentro de la escala; además su numearal romano indica la longitud del intervalo de su localización respecto a la tónica:
| Grado | Nombre | Intervalo desde tónica | Función |
|---|---|---|---|
| I | TÓNICA | Unísono (cons. perfecta) | Tonal |
| II | Supertónica | Segunda mayor (dis. suave) | |
| III | MEDIANTE | Tercera mayor (cons. imperfecta) | Modal |
| IV | Subdominante | Cuarta justa (cons. perfecta) | Tonal |
| V | DOMINANTE | Quinta justa (cons. perfecta) | Tonal |
| VI | Superdominante | Sexta mayor (cons. imperfecta) | Modal |
| VII | SENSIBLE | Séptima mayor (dis. fuerte) | |
| VIII | OCTAVA | Octava (cons. perfecta) | Tonal |
Una escala es la base sobre la cual se asienta la tonalidad, la organización de las notas alrededor de la tónica. En esta tabla se han escrito en mayúsculas los nombres de los grados más importantes de la escala, los cuales corresponden a intervalos consonantes.
En el estudio de los intervalos vimos que existen intervalos consonantes e intervalos disonantes; mientras más consonante sea el intervalos asociado a un grado, más conveniente será este grado para la creación de armonías y mayor será su importancia. Como se verá posteriormente, estos serán los primeros seleccionados para conformar acordes. Tendremos así que el acorde mayor formados sobre el primer grado y los acordes mayores formados sobre el IV y V grados, correspondientes a los intervalos justos de cuarta justa y quinta justa y denominados dominante y subdominante, serán los más importantes en la armonización clásica de la tonalidad correspondiente a la tónica.
Los grados de una escala cumplen una función dentro de la tonalidad. Los grados con una función tonal son el pilar de la tonalidad, mientras que los grados con una función modal definen el modo de la tonalidad; así, como veremos posteriormente, para obtener una escala menor natural a partir de una escala mayor el tercer y sexto grados de la escala mayor se bajan en un semitono, con lo cual sus intervalos correspondientes pasan a ser menores. La tonalidad menor resultante que se obtiene a partir de esta escala es más apropiada para expresar tristeza que su contraparte mayor, más conveniente para expresar alegría. En ambas escalas los grados con función tonal permanecen inalterados.
Otro aspecto importante de los grados de una escala es que pueden presentar una tendencia a llevar a otros grados de la escala, a resolver hacia otro grado; por ejemplo, al oír una secuencia de notas en la que la última correspondiente al grado dominante el oído anticipa (pide) la nota correspondiente al grado tónica.
En lo que sigue es importante conocer la distribución de las notas de la escala mayor de Do sobre el pentagrama:

Escalas menores
La escala mayor ciertamente es la más importante en la música occidental, pero para desarrollar diferentes géneros musicales es necesario recurrir a otros tipos de escala. En esta sección consideraremos las ocupan el segundo lugar en cuanto a la importancia y difusión: las escalas menores.
En la tabla anterior se indicó la función de cada uno de los grados de la escala mayor y se señaló que los grados I, IV, V y VIII tienen una función tonal y una consonancia perfecta, mientras que los grados III y VI tienen una función modal y una consonancia imperfecta. Supongamos que deseamos componer una melodía que tenga como tónica la nota C, pero no deseamos que tenga la sonoridad de las melodías escritas en el modo mayor. Para que esta melodía tenga como centro tonal la nota C, debemos conservar las notas C, F y G, puesto que corresponden a los grados I, IV y V y cumplirán la función tonal; para lograr una sonoridad diferente bajaremos un semitono las notas E y A, puesto que corresponden a los grados III y V y tienen una función modal. Para concluir la construcción de nuestra nueva escala también bajaremos un semitono la nota B, correspondiente al grado VII y evitaremos así la disonancia fuerte que posee con la tónica. Nuestra escala queda entonces en la forma:

La escala que hemos desarrollado es el caso particular para la tónica C de la escala menor natural en la teoría de la música. Su fórmula es:

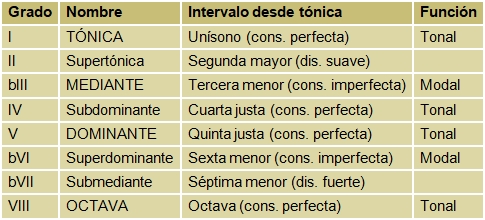
Los nombres de los grados de esta escala y sus correspondientes funciones y consonancias son:
En la sección Una melodía simple de la página correspondiente a la identificación de las notas musicales, usted practicó la melodía "Twinkle, Twinkle Little Star" en la escala de Do mayor. A continuación crearemos un arreglo de esta melodía en el cual utilizaremos la escala de Do menor; esto es, reemplazaremos las notas E4 por D#4 y las notas A4 por G#4. El resultado es el siguiente:

Para facilitar la comparación de esta versión en tono menor con la original en tono mayor, repetimos a continuación el enlace a la versión mayor; pero para una comparación más completa quizás sea más conveniente que usted abra una copia de este sitio en una nueva pestaña de su navegador y vaya a la página Notas musicales.
La opinión generalizada es que las escalas mayores se prestan mejor para expresar alegría y las escalas menores para expresar tristeza. Se trata de algo muy subjetivo, pero probablemente usted estará de acuerdo en que la versión menor de "Twinkle, Twinkle, Little Star" tiene un tono más bien sombrío.
La distribución de las notas de la escala menor de Do sobre el pentagrama es:

Escalas relativas
En esta sección estudiaremos un concepto de suma importancia en la teoría de música: el de escalas relativas.
Si usted realizó correctamente el ejercicio habrá obtenido las mismas notas en ambas escalas: C, D, E, F, G, A y B.
El resultado del ejercicio anterior nos lleva a la conclusión de que a toda escala mayor corresponde una escala relativa menor (natural) que se construye a partir de su grado VI (nueve semitonos después de la tónica; o equivalentemente, tres semitonos antes de la tónica octava) y que posee exactamente las mismas notas; y viceversa: a toda escala menor natural corresponde una escala relativa mayor que posee exactamente sus mismas notas y se construye a partir de su grado bIII (tres semitonos después de la tónica).
El resultado anterior se puede visualizar sobre el pentagrama:

El concepto de escalas relativas es de tal importancia que usted debería poder determinar casi instantáneamente la escala relativa de cualquier escala dada. Se podría haber dado acá una tabla con pares de escalas relativas, pero el autor considera que mucho mejor que memorizar tal tabla es tener presente lo antes dicho: el tono relativo menor se encuentra tres semitonos antes de la tónica y el tono relativo mayor se encuentra tres semitonos después de la tónica. La familiarización con la analogía del reloj permite visualizar instantáneamente las tonalidades relativas; efectivamente, supongamos que estamos interesados en identificar la tonalidad relativa menor de La mayor: basta visualizar la nota A, ubicada a las 9 horas, y la nota F# (3 horas antes); la tonalidad relativa menor de la tonalidad mayor de La es entonces la tonalidad menor natural correspondiente a la nota F#, ubicada a la seis horas.
Una muy buena razón práctica para poder identificar rápidamente tonalidades relativas es que el movimiento entre tonalidades relativas en una composición es sumamente común en toda clase de géneros musicales. Otra razón práctica, y además teórica, la estudiaremos a continuación.
Alteraciones contenidas en escalas
La única escala mayor que no posee alteraciones es la correspondiente a Do, y la única menor natural que no posee alteraciones es su relativa, correspondiente a La. Para poder reconocer la tonalidad en la cual se encuentra una melodía transcrita en la notación clásica es muy importante que conozcamos las alteraciones correspondientes a cada una de las escalas; por tanto a continuación se propone un ejercicio en el cual usted determinará estas alteraciones. El ejercicio consistirá en completar la tabla siguiente:
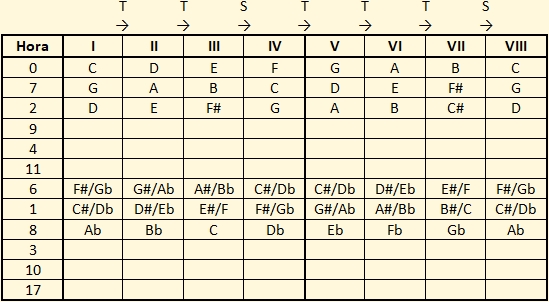
Las siguientes observaciones pueden serle útiles en la realización del ejercicio:
- Para ayudarle a determinar las notas de las escalas se ha agregado la fórmula de las escalas mayores arriba del cuerpo de la tabla.
- La primera columna indica la localización de la tónica sobre la carátula del reloj; este detalle puede serleútil para verificar su trabajo. Por razones que se harán claras al completar el ejercicio, se avanza por intervalos de quintas; o sea, por intervalos de siete horas sobre la carátula del reloj.
- Se han identificado dos grupos de cuatro notas para cada escala, el primero se inicia en el grado tónica (I)y el segundo en el grado dominante (V). El primer grupo de cada escala es exactamente igual al segundo grupo de la escala anterior. Al avanzar en la tabla los sostenidos se incrementan en uno, el cual corresponde a la nota inmediatamente anterior a la tónica considerada (nota sensible).
- Para la escala mayor de Fa sostenido (Sol bemol) se pueden usar tanto sostenidos como bemoles, los cuales posee en igual número: 7.
- Para la escala mayor de Do sostenido Re bemol) se tienen siete sostenidos, o sea que no se incrementó su número, y seis bemoles, o sea que su número se redujo en uno; por tanto, para ésta y para las escalas que siguen lo usual es emplear bemoles.
Armaduras
Al comienzo de la sección anterior señalamos que era necesario conocer la distribución de las alteraciones de las diferentes escalas para poder determinar la tonalidad en la cual se encuentra una melodía escrita en la notación tradicional. El primer símbolo que conseguimos sobre las pautas usadas en la transcripción de una melodía es el correspondiente a la clave, la cual, en esta páginas, cuyo objetivo final es la enseñanza de instrumentos de cuerda, será la clave de Sol. A continuación de la clave se encuentra la armadura, el conjunto de símbolos de alteración que permite identificar la tonalidad en la cual está escrita la melodía. A continuación se muestran las diferentes armaduras, las cuales se obtienen de los resultados del ejercicio anterior; el orden de los las armaduras con bemoles corresponde a las que se obtienen a partir del Do pero bajando por intervalos de quintas; esto es, viajando en sentido contrario al de las manecillas del reloj con saltos de siete horas en la utilidad Analogía del reloj:

Observaciones:
- Existen patrones claramente definidos para la colocación de los sostenidos y de los bemoles; conviene memorizarlos para poder escribir rápidamente la armadura de una tonalidad.
- La tonalidad de Do mayor no contiene accidentes, por tanto no requiere armadura.
- Las armaduras con sostenidos para otras tonalidades se escriben comenzado por el sostenido colocado sobre la línea correspondiente a la nota F# y terminando con el numeral colocado sobre la línea o espacio correspondiente a la nota un tono antes de la tónica.
- Las armaduras con bemoles se escriben comenzado por el bemol colocado sobre la línea correspondiente a la nota Bb y terminando con el bemol colocado sobre la línea o espacio correspondiente a la nota un intervalo de cuarta justa (cinco semitonos)después de la tónica.
- Para identificar la tonalidades que corresponden a una armadura constituida de sostenidos, tome como referencia la nota asociada al último sostenido; las tonalidad serán la mayor que se encuentra medio tono hacia adelante y la relativa menor de esta tonalidad mayor. Por ejemplo, si la armadura es la de tres sostenidos, cuyo último sostenido es el Do sostenido, la tonalidades serán la de Re mayor y su relativa menor de Si bemol.
- Identificar la tonalidades correspondientes a una armadura constituida de bemoles, es aun más fácil: las tonalidades serán la mayor que tiene como tónica a la nota que ocupa el penúltimo lugar y su relativa menor. Por ejemplo, la penúltima nota de la armadura con cuatro bemoles es Ab, por tanto las tonalidades son la mayor de La bemol y su relativa menor de Fa.
Puesto que la metodología explicada para determinar la escalas asociadas a una armadura no distingue cuál de las dos corresponde a la melodía que sigue a la armadura tenemos que dar respuesta a esta interrogante. La respuesta a esta pregunta es que, dependiendo de la melodía, puede ser un análisis de la misma para determinar la nota alrededor de la cual se desarrolla la melodía; esto es, determinar su centro tonal. En estas páginas no estudiaremos la forma de determinar el centro tonal de una melodía o parte de la misma; sin embargo, para melodías simples su oído podrá distinguir si se trata de una melodía en modo mayor o en modo menor, lo cual responderá la interrogante. Ya usted realizó un ejercicio en el cual notó la diferencia entre las versiones en Do mayor y Do menor de "Twinkle, Twinkle, Little Star"; sin embargo, ambas escalas difieren en tres notas, y pudiera no resultar tan fácil discriminar entre la versión de esta melodía en Do mayor y su versión en su relativa La menor, puesto que las escalas de ambas tonalidades poseen las mismas notas. Hagamos un experimento en el cual, para reducir la influencia de su familiarización con el ejercicio anterior en su resultado, usaremos tonalidades diferentes a Do mayor y su relativa La menor.
La escala menor armónica
La escala menor natural tiene el problema de que su séptimo grado se encuentra a un tono completo de la tónica octava, por lo cual no conduce a la tónica con la misma fuerza que el séptimo grado de la escala mayor, así que la escala menor es menos concluyente que la escala mayor. Observe que esta diferencia se refleja en los nombre diferentes dados a este grado en ambas escalas: sensible en la escala mayor, submediante en la escala menor. La solución dada a este problema es la de elevar un semitono el grado séptimo de la escala menor natural para obtener una nueva escala: la escala menor armónica, en la cual el séptimo grado pasa a llamarse sensible. Este cambio, si bien soluciona un problema, acarrea también consecuencias. Una de ellas es que ahora existe una separación de tres semitonos entre las grados tal y como veremos en la página siguiente, dedicada a los acordes y la armonización de las escalas.
A continuación se muestra la escala menor armónica para Do:

La escala menor melódica
Si bien la escala menor armónica soluciona el problema de la resolución hacia la tónica, acarrea también consecuencias. Una de ellas es que ahora existe una separación de tres semitonos entre las notas correspondientes a los grados VI y VII, lo cual no es conveniente desde el punto de vista de la melodía, y otra es que afecta la armonización de la escala, tal y como veremos en la página siguiente, dedicada a los acordes y la armonización de las escalas.
Para resolver la primera dificultad, se usa una tercera escala menor: la escala menor melódica, en la cual elimina la disminución de un semitono de la nota correspondiente al sexto grado de la escala menor armónica, acercándola a sólo un tono de la nota correspondiente al séptimo grado. A continuación se muestra el ascenso sobre la escala menor melódica para Do:

Observe que se muestra una flecha para indicar ascenso a través de la escala. La razón para hacer hincapié en este hecho es que al descender la escala se usa la nota Ab correspondiente al grado bVI, lo cual da una mejor resolución hacia el quinto grado, un grado sumamente importante. De acuerdo con esto, la escala mostrada en la figura anterior corresponde a la escala menor melódica ascendente. Por otro lado, la escala melódica descendente coincide exactamente con la escala menor natural ejecutada en forma descendente.

Comparación de escalas
La siguiente tabla puede ser muy útil para efectos de referencia y afianzar lo aprendido respecto a las escalas:
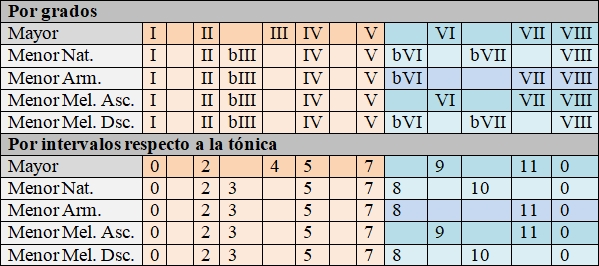
Observe que:
- Para efectos de comparación es conveniente separar las escalas en sus cinco notas bajas y sus tres notas altas.
- Las cinco notas bajas de las escalas menores son todas iguales y difieren de las cinco notas bajas de las escalas mayores sólo en la disminución del tercer grado en un semitono.
- Las tres notas altas de la escala menor armónica difieren de las tres notas altas de la escala menor natural sólo en que no se baja en un semitono la nota correspondiente al séptimo grado.
- Las tres notas altas de la escala menor melódica difieren de las tres notas altas de la escala menor armónica sólo en que no se baja en un semitono la nota correspondiente al sexto grado.
- Las tres notas altas de la escala menor melódica son idénticas a las de la escala menor natural.
En la tabla se resaltan estas similitudes y diferencias mediante el uso de colores.
Deducción de la tonalidad de una melodía
A continuación presentamos la transcripción de un arreglo simple de la melodía de "Greensleeves" en la tonalidad de La menor:

Como la armadura empleada no contiene alteraciones, deducimos que la melodía se encuentra en Do mayor o en La menor. Su tono más bien triste y de queja nos sugiere fuertemente que debe estar en el modo menor. El hecho de que las dos primeras frases musicales comiencen en la nota A y terminen en la nota E, intervalo de quinta (siete horas) es un indicativo todavía más fuerte; pero si deseamos saberlo con certeza, y además el tipo de escala menor que emplea, debemos analizarla. Para ello elaboramos la siguiente tabla en la cual se identifican los grados de cada una de sus notas:

Para facilitar la comparación procederemos a ordenar, sin repeticiones, los grados y los intervalos empleados en esta melodía:

Se ve claramente que esta melodía emplea la escala menor melódica, puesto que es la única, en su combinación de ascenso y descenso, que emplea los grados bVI, VI, bVII y VII. Las otras escalas menores emplean sólo dos de estos grados.
NOTA: en realidad no hace falta emplear los intervalos, pero el hecho de que la numeración arábiga sea bastante más simple que la romana simplifica la comparación.
Varios
.